
More References and Links to Geometry Geometry Tutorials, Problems and Interactive Applets. The two solutions correspond to two congruent right triangles.We now calculate the lengths of AB and CB.Two solutionsĢA = 31.6 degrees (nearest tenth) or A = 15.8 degreesĢA = 148.4 degrees (nearest tenth) or A = 74.2 degrees The central angle theorem states that the central angle from two chosen points on the circle is always twice the inscribed angle from those two points. The area At might also be written as follows (using the identity sin(2A) = 2 sin (A) cos (A)).Īt = (1/2) * AB * CB = 200 cos (A) sin(A) = 100 sin (2A) = 50 Pi / 3.Sin(A) = CB / AC = CB / 20 which gives CB = 20 sin (A)Īnd cos(A) = AB / AC = AB / 20 which gives AB = 20 cos (A) Since triangle ABC has a right angle, we now use the internal angle (to the triangle) A to write.
If At is the area of triangle ABC and As the shaded area then we need to have As = 2 At.Īt + As = (1/2) area of circle = (1/2) Pi 10 2 = 50 Pi
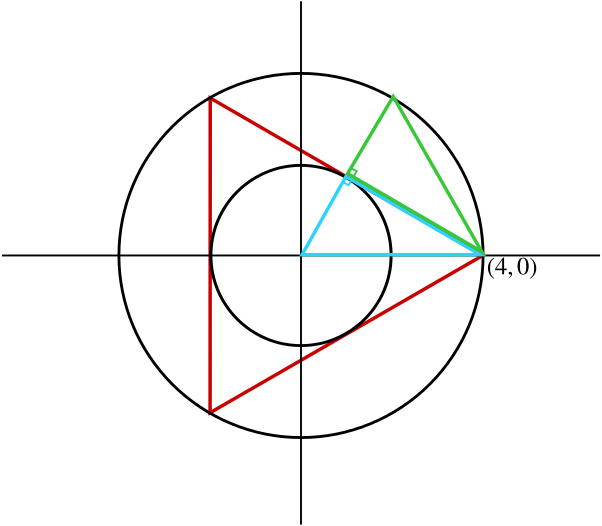
Find the lengths of AB and CB so that the area of the the shaded region is twice the area of the triangle.

In the figure below, triangle ABC is a triangle inscribed inside the circle of center O and radius r = 10 cm. Inscribed right triangle problem with detailed solution. Triangle Inscribed in a Circle - Problem With Solution


 0 kommentar(er)
0 kommentar(er)
